The Bernstein polynomials are very pretty, and very useful for evaluation of the curve.
The value at these Bernstein polynomial at the endpoints.
The derivative of these Bernstein polynomials.
The derivative of these Bernstein polynomials at the endpoints.
Plots of the derivatives of these Bernstein polynomials.
The value of these equations is a nice simple zero/one at the endpoints. But the derivatives are slightly more complicated. Instead a simple linear combinations gives a very nice value/derivative breakdown, called the cubic Hermite spline basis functions.
The value of these Hermite spline basis polynomials at the endpoints.
The derivative of these Hermite spline basis polynomials.
The derivative of these Hermite spline basis polynomials at the endpoints.
We can construct a polynomial as a linear combination of these four cubics easily.
So the first curve is all of the value at the initial endpoint.
The second curve is all of the derivative at the initial endpoint.
The third curve is all of the derivative at the final endpoint.
The fourth curve is all of the value at the final endpoint.






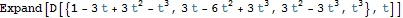


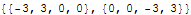







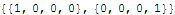


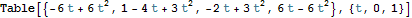


No comments:
Post a Comment