a couple useful properties of cubic bezier curves

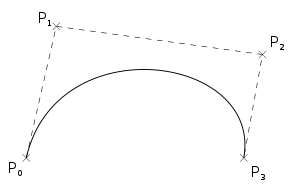
The cubic Bezier with control points p0, p1, p2, p3 has a number of useful properties.

• The path interpolates between the first and the last control points, p0 and p3.
• The tangent line at p0 is in the direction of p1.  The Bernstein formulation shows us that the magnitude of the tangent is the distance from p0 to p1.
• The tangent line at p3 is in the (negative of the) direction of p2. The Bernstein formulation shows us that the magnitude of the tangent is the distance from p2 to p3.
• The De Casteljau method of drawing these curves shows that the curve is a affine combination of the four control points.  So the curve will be within the convex hull of the control points.
• Because the curve is an affine combination of the control points, the linear transformation of a Bezier curve is the Bezier curve defined by the linear transformations of its control points. (e.g. rotation and translation of the control points causes the same rotation and translation of the curve)