subdividing a cubic bezier curve

Another useful property of a cubic Bezier is that it can be perfectly subdivided into two smaller cubic splines at any point.

This is a change of variables, remapping the first segment {0..t} -> {0..1} and the second segment {t..1} -> {0..1}

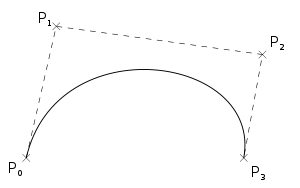
For a cubic Bezier spline with control points P0, P1, P2, P3. We can evaluate a point on the curve with De Casteljau's algorithm:

Q0[t_] := P0 * (1 - t) + P1 *t
Q1[t_] := P1 * (1 - t) + P2 *t
Q2[t_] := P2 * (1 - t) + P3 *t

R0[t_] := Q0[t] * (1 - t) + Q1[t] * t
R1[t_] := Q1[t] * (1 - t) + Q2[t] * t

S0[t_] := R0[t] * (1 - t) + R1[t] * t

In the wikipedia graphics below S0 is shown as B.



We subdivide the curve into two segments at any value t.  The first segment will have control points P0, Q0[t], R0[t], S0[t].  The second will have control points S0[t], R1[t], Q2[t], P3.

Recursively subdividing the cubic spline with t=0.5 is a good numerically stable way of drawing these curves.  (The recursion is halted at the display resolution, or when the curve segment between the endpoints is sufficiently straight.)

a couple useful properties of cubic bezier curves

The cubic Bezier with control points p0, p1, p2, p3 has a number of useful properties.

• The path interpolates between the first and the last control points, p0 and p3.
• The tangent line at p0 is in the direction of p1.  The Bernstein formulation shows us that the magnitude of the tangent is the distance from p0 to p1.
• The tangent line at p3 is in the (negative of the) direction of p2. The Bernstein formulation shows us that the magnitude of the tangent is the distance from p2 to p3.
• The De Casteljau method of drawing these curves shows that the curve is a affine combination of the four control points.  So the curve will be within the convex hull of the control points.
• Because the curve is an affine combination of the control points, the linear transformation of a Bezier curve is the Bezier curve defined by the linear transformations of its control points. (e.g. rotation and translation of the control points causes the same rotation and translation of the curve)

an interactive svg interpolation example

This svg example simulates dragging of the four points to be interpolated, using Bezier control points p_0, p_1, p_2, p_3, interpolating f[0],f[1],f[2],f[3]
p_0 = f[0]
p_1 = 1/6 (-5 f[0]+18 f[1]-9 f[2]+2 f[3])
p_2 = 1/6 (2 f[0]-9 f[1]+18 f[2]-5 f[3])
p_3 = f[3]

There exist other interpolations of these points.

interpolating using bezier splines

We will often want to use splines to model other data.  There are two modeling, interpolation and approximation. 

Wikipedia states: interpolation is a method of constructing new data points within the range of a discrete set of known data points.

A cubic Bezier spline segment, as a cubic polynomial can perfectly interpolate four points.

Finding the interpolating cubic polynomial for a set of four data points is a special case of more general polynomial interpolation.

The most direct form of this polynomial interpolation is to directly plug into this Lagrange basis functions for y=y[0],y[1],y[2],y[3] at t=0,1/3,2/3,1.

In this way, y = y[0] + t^2 (9 y[0] - (45 y[1])/2 + 18 y[2] - (9 y[3])/2) +
 t (-((11 y[0])/2) + 9 y[1] - (9 y[2])/2 + y[3]) +
 t^3 (-((9 y[0])/2) + (27 y[1])/2 - (27 y[2])/2 + (9 y[3])/2) and similarly for x.

When we expand into standard polynomial form we get:
x[t_]:= a_x + t * b_x + t^2 * c_x + t^3 *d_x
y[t_]:= a_y + t * b_y + t^2 * c_y + t^3 *d_y

giving

a_y = y[0]
b_y = (-((11 y[0])/2) + 9 y[1] - (9 y[2])/2 + y[3])
c_y = (9 y[0] - (45 y[1])/2 + 18 y[2] - (9 y[3])/2)
d_y = (-((9 y[0])/2) + (27 y[1])/2 - (27 y[2])/2 + (9 y[3])/2)

When we put this into the form of Bezier control points:

for f[0]={x[0],y[0]}, {x[1],y[1]}, {x[2],y[2]}, {x[3],y[3]}

p_0 = f[0]
p_1 = 1/6 (-5 f[0]+18 f[1]-9 f[2]+2 f[3])
p_2 = 1/6 (2 f[0]-9 f[1]+18 f[2]-5 f[3])
p_3 = f[3]