an interactive svg example

This svg example simulates dragging of the four control points. The starting position is the same as the example used in other posts.

A cubic spline example

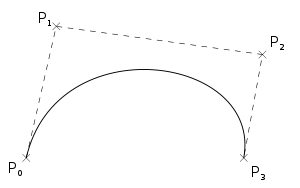The example at left is taken from wikipedia and I'd like to talk about it. The original code for the graphics contain the curve as

<path d="M 70,420 C 150,70 700,145 650,420" style="fill: none; stroke-width: 2.5; stroke: black;"></path>

The details of the syntax are defined in the SVG Path specification.

Point	x	y
P0	70	420
P1	150	70
P2	700	145
P3	650	420

We can evaluate this with the De Casteljau's algorithm:

Q0[t_] := P0 * (1 - t) + P1 *t
Q1[t_] := P1 * (1 - t) + P2 *t
Q2[t_] := P2 * (1 - t) + P3 *t

R0[t_] := Q0[t] * (1 - t) + Q1[t] * t
R1[t_] := Q1[t] * (1 - t) + Q2[t] * t

S0[t_] := R0[t] * (1 - t) + R1[t] * t

and plot S0[t] over the range {t,0,1}.  In the wikipedia graphics below S0 is shown as B.




The name of them though is cubic spline.  So let's get it into cubic form.  These control points are in fact the coefficients of Bernstein polynomial of degree 3. 

b_{0,3}[t] = (1 - t)^3
$b\_\{1,3\}[t]\; =\; 3t(1\; -\; t)^2$
$b\_\{2,3\}[t]\; =\; 3t^2(1\; -\; t)$
$b\_\{3,3\}[t]\; =\; t^3$

and the spline segment is:

B[t] = b_{0,3}[t] * P0 +  b_{1,3}[t] * P1 + b_{2,3}[t] * P2 +  b_{3,3}[t] * P3

this can be expanded into separate x and y components:

x[t] = b_{0,3}[t] * P0_x + b_{1,3}[t] * P1_x + b_{2,3}[t] * P2_x + b_{3,3}[t] * P3_x
y[t] = b_{0,3}[t] * P0_y + b_{1,3}[t] * P1_y + b_{2,3}[t] * P2_y + b_{3,3}[t] * P3_y

When we expand into standard polynomial form we get:
x[t_]:= a_x + t * b_x + t^2 * c_x + t^3 *d_x
y[t_]:= a_y + t * b_y + t^2 * c_y + t^3 *d_y

where

a_x = P0_x
b_x = 3* P1_x - 3 P0_x
c_x = 3*P2_x - 6 *P1_x + 3*P0_x
d_x = P3_x - 3 * P2_x + 3*P1_x - P0_x

and similarly

a_y = P0_y
b_y = 3* P1_y - 3 P0_y
c_y = 3*P2_y - 6 *P1_y + 3*P0_y
d_y = P3_y - 3 * P2_y + 3*P1_y - P0_y

why splines?

I've been fascinated with splines for about 20 years. 

Years back I spent a lot of time starting at the spline art on the front cover of PostScript Language Tutorial and Cookbook. It wasn't until years later that I would understand enough math or have good enough explanations to understand.




But I now have enough math to understand.  And like all hobbies I get pleasure from talking about it and fiddling with it.

The splines that are most common these days are cubic Bézier splines (the wikipedia page Bézier curve has better pictures).  They find use in CAD (a lot of the original work was done for the auto industry), fonts, and animation.  Basically they're the goto solution where smooth curves are desired.